XGBoost是陈天奇于2014年提出的一套并行boost算法的工具库, LightGBM是微软推出的boosting框架, CatBoost是Yandex推出的Boost工具包. 本文将对这些算法进行介绍,并在数据集上对算法进行测试.

XGBoost

简介

XGBoost的全称是eXtreme Gradient Boosting，既可以用于分类也可以用于回归问题中, 它是经过优化的分布式梯度提升库，旨在高效、灵活且可移植。XGBoost是大规模并行boosting tree的工具，它是目前最快最好的开源 boosting tree工具包，比常见的工具包快10倍以上。在数据科学方面，有大量的Kaggle选手选用XGBoost进行数据挖掘比赛，是各大数据科学比赛的必杀武器；在工业界大规模数据方面，XGBoost的分布式版本有广泛的可移植性，支持在Kubernetes、Hadoop、SGE、MPI、 Dask等各个分布式环境上运行，使得它可以很好地解决工业界大规模数据的问题。

什么是 Gradient Boosting

Gradient boosting 是 boosting 的其中一种方法. 所谓 Boosting, 就是将弱分离器 $f_i(X)$ 组合起来形成强分类器 F(X) 的一种方法。

所以 Boosting 有三个要素:

• A loss function to be optimized: 例如分类问题中用 cross entropy，回归问题用 mean squared error
• A weak learner to make predictions: 例如决策树
• An additive model: 将多个弱学习器累加起来组成强学习器，进而使目标损失函数达到极小

Gradient boosting 就是通过加入新的弱学习器，来努力纠正前面所有弱学习器的残差，最终这样多个学习器相加在一起用来进行最终预测，准确率就会比单独的一个要高。之所以称为 Gradient，是因为在添加新模型时使用了梯度下降算法来最小化的损失。

另一种 Gradient Boosting 的实现就是 AdaBoost（Adaptive Boosting）。 AdaBoost 就是将多个弱分类器，通过投票的手段来改变各个分类器的权值，使分错的分类器获得较大权值。同时在每一次循环中也改变样本的分布，这样被错误分类的样本也会受到更多的关注。

为什么使用 XGBoost

XGBoost 是对 gradient boosting decision tree 的实现，但是一般来说，gradient boosting 的实现是比较慢的，因为每次都要先构造出一个树并添加到整个模型序列中。而 XGBoost 的特点就是计算速度快，模型表现好，这两点也正是项目的目标。

表现快是因为它具有这样的设计：

• Parallelization：训练时可以用所有的 CPU 内核来并行化建树。
• Distributed Computing：用分布式计算来训练非常大的模型。
• Out-of-Core Computing：对于非常大的数据集还可以进行 Out-of-Core Computing。
• Cache Optimization of data structures and algorithms：更好地利用硬件资源。

应用

使用方式

使用xgboost库有两种方式：

第一种方式，直接使用xgboost库的建模流程

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

import xgboost as xgb

# 第一步，读取数据
xgb.DMatrix()

# 第二步，设置参数
param = {}

# 第三步，训练模型
bst = xgb.train(param)

# 第四步，预测结果
bst.predict()

​ 其中最核心的，是DMtarix这个读取数据的类，以及train()这个用于训练的类。与sklearn把所有的参数都写在类中的方式不同，xgboost库中必须先使用字典设定参数集，再使用train来将参数及输入，然后进行训练。会这样设计的原 因，是因为XGB所涉及到的参数实在太多，全部写在xgb.train()中太长也容易出错。 params可能的取值以及xgboost.train的参数如下：

params {eta, gamma, max_depth, min_child_weight, max_delta_step, subsample, colsample_bytree, colsample_bylevel, colsample_bynode, lambda, alpha, tree_method string, sketch_eps, scale_pos_weight, updater, refresh_leaf, process_type, grow_policy, max_leaves, max_bin, predictor, num_parallel_tree}

xgboost.train (params, dtrain, num_boost_round=10, evals=(), obj=None, feval=None, maximize=False, early_stopping_rounds=None, evals_result=None, verbose_eval=True, xgb_model=None, callbacks=None, learning_rates=None)

第二种方式，使用xgboost库中的sklearn的API。

​ 可以调用如下的类，并用 sklearn当中惯例的实例化，fit和predict的流程来运行XGB，并且也可以调用属性比如coef_等等。

1

class xgboost.XGBRegressor (max_depth=3, learning_rate=0.1, n_estimators=100, silent=True, objective='reg:linear', booster='gbtree', n_jobs=1, nthread=None, gamma=0, min_child_weight=1, max_delta_step=0, subsample=1, colsample_bytree=1, colsample_bylevel=1, reg_alpha=0, reg_lambda=1, scale_pos_weight=1, base_score=0.5, random_state=0, seed=None, missing=None, importance_type='gain', **kwargs)

调用xgboost.train和调用sklearnAPI中的类XGBRegressor，需要输入的参数是不同的，而且看起来相当的不同。但 其实，这些参数只是写法不同，功能是相同的。比如说，我们的params字典中的第一个参数eta，其实就是我们 XGBRegressor里面的参数learning_rate，他们的含义和实现的功能是一模一样的。只不过在sklearnAPI中，开发团 队友好地帮助我们将参数的名称调节成了与sklearn中其他的算法类更相似的样子。

​ XGBoost本身的核心是基于梯度提升树实现的集成算法，整体来说可以有三个核心部分：集成算法本身，用于集成的弱评估器，以及应用中的其他过程。三个部分中，前两个部分包含了XGBoost的核心原理以及数学过程，最后的部分主要是在XGBoost应用中占有一席之地。

参数介绍

选择弱评估器：重要参数 booster

梯度提升算法中不只有梯度提升树，XGB作为梯度提升算法的进化，自然也不只有树模型一种弱评估器。在XGB中， 除了树模型，还可以选用线性模型，比如线性回归，来进行集成。虽然主流的XGB依然是树模型，但也可以 使用其他的模型。基于XGB的这种性质，有参数“booster"来控制使用怎样的弱评估器。

两个参数都默认为"gbtree"，如果不想使用树模型，则可以自行调整。当XGB使用线性模型的时候，它的许多数学过程就与使用普通的Boosting集成非常相似。

XGB的目标函数：重要参数objective

梯度提升算法中都存在着损失函数。不同于逻辑回归和SVM等算法中固定的损失函数写法，集成算法中的损失函数是可选的，要选用什么损失函数取决于我们希望解决什么问题，以及希望使用怎样的模型。比如说，如果我们的目标是进行回归预测，那我们可以选择调节后的均方误差RMSE作为我们的损失函数。如果我们是进行分类预测，那我们可以选择错误率error或者对数损失log_loss。只要我们选出的函数是一个可微的，能够代表某种损失的函数，它就可以是我们XGB中的损失函数。

在众多机器学习算法中，损失函数的核心是衡量模型的泛化能力，即模型在未知数据上的预测的准确与否，我们训练模型的核心目标也是希望模型能够预测准确。在XGB中，准确预测自然是非常重要的因素，但需注意，XGB 是实现了模型表现和运算速度的平衡的算法。普通的损失函数，比如错误率，均方误差等，都只能够衡量模型的表现，无法衡量模型的运算速度。许多模型中使用空间复杂度和时间复杂度来衡量模型的运算效 率。XGB因此引入了模型复杂度来衡量算法的运算效率。因此XGB的目标函数被写作：传统损失函数 + 模型复杂度。

$$ Obj = \sum_{i=1}^ml(y_i,\hat{y_i}) + \sum_{k=1}^K\Omega(f_k) $$

其中$i$代表数据集中的第 $i$ 个样本，$m$ 表示导入第 $k$ 棵树的数据总量，$K$ 代表建立的所有树(n_estimators)，当只建立了 $t$ 棵树的时候，式子应当为 $\sum_{k=1}^t\Omega(f_k)$。第一项代表传统的损失函数，衡量真实标签 $y_i$ 与预测值 $\hat{y_i}$ 之间的差异，通常是RMSE调节后的均方误差。第二项代表模型的复杂度，使用树模型的某种变换 $\Omega$ 表示，这个变化代表了一个从树的结构来衡量树模型的复杂度的式子，可以有多种定义。注意，我们的第二项中没有特征矩阵 $x_i$ 的介入。我们在迭代 每一棵树的过程中，都最小化 Obj 来力求获取最优的 $\hat{y}$ ，因此我们同时最小化了模型的错误率和模型的复杂度，这种 设计目标函数的方法不得不说实在是非常巧妙和聪明。

还可以从另一个角度去理解目标函数,即方差-偏差困境。在机器学习中，用来衡量模型在未知数据上的准确率的指标，叫做泛化误差（Genelization error）。一个集成模型(f) 在未知数据集(D)上的泛化误差 $E(f;D)$ ，由方差(var)，偏差(bais)和噪声 $\varepsilon$共同决定，泛化误差越小，模型就越理想。从下面的图可以看出来，方差和偏差是此消彼长的，并且模型的复杂度越高，方差越大，偏差越小。

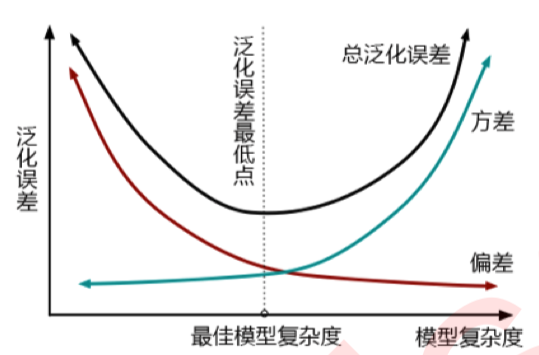
方差可以被简单地解释为模型在不同数据集上表现出来地稳定性，而偏差是模型预测的准确度。那方差-偏差困境就可以对应到 Obj 中了:

$$ Obj = \sum_{i=1}^ml(y_i,\hat{y_i}) + \sum_{k=1}^K\Omega(f_k) $$

第一项是衡量我们模型的偏差，模型越不准确，第一项就会越大。第二项是衡量我们的方差，模型越复杂，模型的学习就会越具体，到不同数据集上的表现就会差异巨大，方差就会越大。所以我们求解的最小值，其实是在求解方差与偏差的平衡点，以求模型的泛化误差最小，运行速度最快。我们知道树模型和树的集成模型都是学习天才，是天生过拟合的模型，因此大多数树模型最初都会出现在图像的右上方，我们必须通过剪枝来控制模型不要过拟合。现在 XGBoost的损失函数中自带限制方差变大的部分，也就是说XGBoost会比其他的树模型更加聪明，不会轻易落到图像的右上方。可见，这个模型在设计的时候的确是考虑了方方面面，难怪XGBoost会如此强大了。

在应用中，我们使用参数“objective"来确定我们目标函数的第一部分中的 $l(y_i, \hat{y_i})$ ，也就是衡量损失的部分。

常用的选择有：

还可以选择自定义损失函数。比如说，我们可以选择输入平方损失 $l(y_i, \hat{y_i} = (y_i - \hat{y_i})^2)$，此时XGBoost 其实就是算法梯度提升机器（gradient boosted machine）。在xgboost中，我们被允许自定义损失函数，但通常我们还是使用类已经为我们设置好的损失函数。回归类中本来使用的就是reg:linear，因此在这里无需做任何调整。注意：分类型的目标函数导入回归类中会直接报错。现在来试试看xgb自身的调用方式。

由于xgb中所有的参数都需要自己的输入，并且objective参数的默认值是二分类，因此我们必须手动调节。

正则化参数

对每一棵树，它都有自己独特的结构，这个结构即是指叶子节点的数量，树的深度，叶子的位置等等所形成的一个可以定义唯一模型的树结构。在这个结构中，我们使用 $q(x_i)$表示样本$x_i$ 所在的叶子节点，并且使用$w_{q(x_i)}$ 来表示这个样本落到第 t棵树上的第$q(x_i)$ 个叶子节点中所获得的分数，于是有：

$$ f_t(x_i) = w_{q(x_i)} $$

这是对于每一个样本而言的叶子权重，然而在一个叶子节点上的所有样本所对应的叶子权重是相同的。设一棵树上总共包含了T个叶子节点，其中每个叶子节点的索引为j ，则这个叶子节点上的样本权重是$w_j$ 。依据这个，我们定义模型的复杂度$\Omega(f)$为（注意这不是唯一可能的定义，我们当然还可以使用其他的定义，只要满足叶子越多/深度越大， 复杂度越大的理论，可以自己决定要是一个怎样的式子）：

$$ \Omega(f) = \gamma T + 正则项(Regularization) $$

如果使用$L2$正则项：

$$ = \gamma T + \frac 1{2} \lambda|w|^2 $$

$$ =\gamma T + \frac 1{2} \lambda \sum_{j=1}^T w_j^2 $$

如果使用$L1$正则项：

$$ = \gamma T + \frac 1{2} \alpha|w| $$

$$ =\gamma T + \frac 1{2} \alpha \sum_{j=1}^T |w_j| $$

还可以两个一起使用：

$$ =\gamma T + \frac 1{2} \alpha \sum_{j=1}^T |w_j| + \frac 1{2} \lambda \sum_{j=1}^T w_j^2 $$

这个结构中有两部分内容，一部分是控制树结构的$\gamma T$ ，另一部分则是我们的正则项。叶子数量 可以代表整个树结构，这是因为在XGBoost中所有的树都是CART树（二叉树），所以我们可以根据叶子的数量判断出树的深度，而 $\gamma$是我们自定的控制叶子数量的参数。

至于第二部分正则项，类比一下岭回归和Lasso的结构，参数 $\alpha$ 和 $\lambda$ 的作用其实非常容易理解，他们都是控制正则化强度的参数，我们可以二选一使用，也可以一起使用加大正则化的力度。当 $\alpha$ 和 $\lambda$ 都为0的时候，目标函数就是普通的梯度提升树的目标函数。

来看正则化系数分别对应的参数：

对于两种正则化如何选择的问题，从XGB的默认参数来看，优先选择的是L2正则化。当然，如果想尝试L1也不是不可。两种正则项还可以交互，因此这两个参数的使用其实比较复杂。在实际应用中，正则化参数往往不是调参的最优选择，如果真的希望控制模型复杂度，通常会调整 $\gamma$ 而不是调整这两个正则化参数，因此不必过于在意这两个参数最终如何影响了模型效果。对于树模型来说，还是剪枝参数地位更高更优先。如果希望调整 $\lambda$ 和 $\gamma$ ，我们往往会使用网格搜索来帮助我们。

让树停止生长：重要参数gamma

从目标函数和结构分数之差 的式子中来看， $\gamma$ 是我们每增加一片叶子就会被剪去的惩罚项。增加的叶子越多，结构分数之差会被惩罚越重，所以 $\gamma$ 又被称之为是“复杂性控制”（complexity control），所以 $\gamma$ 是我们用来防止过拟合的重要参数。实践证明， $\gamma$是对梯度提升树影响最大的参数之一，其效果丝毫不逊色于n_estimators和防止过拟合的神器max_depth。同时， $\gamma$ 还是我们让树停止生长的 重要参数。

可以直接通过设定$\gamma$ 的大小来让XGB中的树停止生长。 $\gamma$ 因此被定义为，在树的叶节点上进行进一步分枝所 需的最小目标函数减少量，$\gamma$ 设定越大，算法就越保守，树的叶子数量就越少，模型的复杂度就越低。

过拟合：剪枝参数与回归模型调参

作为天生过拟合的模型，XGBoost应用的核心之一就是减轻过拟合带来的影响。作为树模型，减轻过拟合的方式主要 是靠对决策树剪枝来降低模型的复杂度，以求降低方差。影响重大的参数还有以下的专用于剪枝的参数：

这些参数中，树的最大深度是决策树中的剪枝法宝，算是最常用的剪枝参数，不过在XGBoost中，最大深度的功能与 参数 $\gamma$ 相似，因此如果先调节了$\gamma$ ，则最大深度可能无法展示出巨大的效果。当然，如果先调整了最大深度，则 $\gamma$ 也有可能无法显示明显的效果。通常来说，这两个参数中我们只使用一个，不过两个都试试也没有坏处。

三个随机抽样特征的参数中，前两个比较常用。在建立树时对特征进行抽样其实是决策树和随机森林中比较常见的一 种方法，但是在XGBoost之前，这种方法并没有被使用到boosting算法当中过。Boosting算法一直以抽取样本（横向 抽样）来调整模型过拟合的程度，而实践证明其实纵向抽样（抽取特征）更能够防止过拟合。

参数min_child_weight不太常用，它是一片叶子上的二阶导数$h_i$ 之和，当样本所对应的二阶导数很小时，比如说为 0.01，min_child_weight若设定为1，则说明一片叶子上至少需要100个样本。本质上来说，这个参数其实是在控制叶子上所需的最小样本量，因此对于样本量很大的数据会比较有效。如果样本量很小（比如使用的波士顿房价数据集，则这个参数效用不大）。就剪枝的效果来说，这个参数的功能也被 $\gamma$替代了一部分，通常来说会试试看这个参数，但这个参数不是优先选择。

通常当我们获得了一个数据集后，我们先使用网格搜索找出比较合适的n_estimators和eta组合，然后使用gamma或者max_depth观察模型处于什么样的状态（过拟合还是欠拟合，处于方差-偏差图像的左边还是右边?），最后再决定是否要进行剪枝。通常来说，对于XGB模型，大多数时候都是需要剪枝的。

样本不均衡

调节样本不平衡的参数scale_pos_weight，这个参数非常类似于之前随机森林和支持向量机中 我们都使用到过的class_weight参数，通常我们在参数中输入的是负样本量与正样本量之比$\frac {sum(negative instances)}{sum(positive instances)}$

LightGBM

简介

GBDT (Gradient Boosting Decision Tree) 是机器学习中一个长盛不衰的模型，其主要思想是利用弱分类器（决策树）迭代训练以得到最优模型，该模型具有训练效果好、不易过拟合等优点。GBDT 不仅在工业界应用广泛，通常被用于多分类、点击率预测、搜索排序等任务；在各种数据挖掘竞赛中也是致命武器，据统计Kaggle上的比赛有一半以上的冠军方案都是基于 GBDT。而 LightGBM（Light Gradient Boosting Machine）是一个实现 GBDT 算法的框架，支持高效率的并行训练，并且具有更快的训练速度、更低的内存消耗、更好的准确率、支持分布式可以快速处理海量数据等优点。

为什么使用LightGBM

常用的机器学习算法，例如神经网络等算法，都可以以mini-batch的方式训练，训练数据的大小不会受到内存限制。而GBDT在每一次迭代的时候，都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小；如果不装进内存，反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据，普通的GBDT算法是不能满足其需求的。

LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题，让GBDT可以更好更快地用于工业实践。

XGBoost的不足及LightGBM的优化

XGBoost的不足

在LightGBM提出之前，最有名的GBDT工具就是XGBoost了，它是基于预排序方法的决策树算法。这种构建决策树的算法基本思想是：首先，对所有特征都按照特征的数值进行预排序。其次，在遍历分割点的时候用 O(data) 的代价找到一个特征上的最好分割点。最后，在找到一个特征的最好分割点的条件下，将数据分裂成左右子节点。

这样的预排序算法的优点是能精确地找到分割点。但是缺点也很明显：首先，空间消耗大。这样的算法需要保存数据的特征值，还保存了特征排序的结果（例如，为了后续快速的计算分割点，保存了排序后的索引），这就需要消耗训练数据两倍的内存。其次，时间上也有较大的开销，在遍历每一个分割点的时候，都需要进行分裂增益的计算，消耗的代价大。最后，对cache优化不友好。在预排序后，特征对梯度的访问是一种随机访问，并且不同的特征访问的顺序不一样，无法对cache进行优化。同时，在每一层长树的时候，需要随机访问一个行索引到叶子索引的数组，并且不同特征访问的顺序也不一样，也会造成较大的cache miss。

LightGBM的优化

为了避免上述XGBoost的缺陷，并且能够在不损害准确率的条件下加快GBDT模型的训练速度，lightGBM在传统的GBDT算法上进行了如下优化：

• 基于Histogram的决策树算法
• 单边梯度采样 Gradient-based One-Side Sampling(GOSS)：使用GOSS可以减少大量只具有小梯度的数据实例，这样在计算信息增益的时候只利用剩下的具有高梯度的数据就可以了，相比XGBoost遍历所有特征值节省了不少时间和空间上的开销
• 互斥特征捆绑 Exclusive Feature Bundling(EFB)：使用EFB可以将许多互斥的特征绑定为一个特征，这样达到了降维的目的
• 带深度限制的Leaf-wise的叶子生长策略：大多数GBDT工具使用低效的按层生长 (level-wise) 的决策树生长策略，因为它不加区分的对待同一层的叶子，带来了很多没必要的开销。实际上很多叶子的分裂增益较低，没必要进行搜索和分裂。LightGBM使用了带有深度限制的按叶子生长 (leaf-wise) 算法
• 直接支持类别特征(Categorical Feature)
• 支持高效并行
• Cache命中率优化

LightGBM的优缺点

优点

速度更快

• LightGBM 采用了直方图算法将遍历样本转变为遍历直方图，极大的降低了时间复杂度
• LightGBM 在训练过程中采用单边梯度算法过滤掉梯度小的样本，减少了大量的计算
• LightGBM 采用了基于 Leaf-wise 算法的增长策略构建树，减少了很多不必要的计算量
• LightGBM 采用优化后的特征并行、数据并行方法加速计算，当数据量非常大的时候还可以采用投票并行的策略
• LightGBM 对缓存也进行了优化，增加了缓存命中率

内存更小

• XGBoost使用预排序后需要记录特征值及其对应样本的统计值的索引，而 LightGBM 使用了直方图算法将特征值转变为 bin 值，且不需要记录特征到样本的索引，将空间复杂度从 O(2*data) 降低为 O(bin) ，极大的减少了内存消耗
• LightGBM 采用了直方图算法将存储特征值转变为存储 bin 值，降低了内存消耗
• LightGBM 在训练过程中采用互斥特征捆绑算法减少了特征数量，降低了内存消耗

缺点

• 可能会长出比较深的决策树，产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度限制，在保证高效率的同时防止过拟合
• Boosting族是迭代算法，每一次迭代都根据上一次迭代的预测结果对样本进行权重调整，所以随着迭代不断进行，误差会越来越小，模型的偏差（bias）会不断降低。由于LightGBM是基于偏差的算法，所以会对噪点较为敏感
• 在寻找最优解时，依据的是最优切分变量，没有将最优解是全部特征的综合这一理念考虑进去

应用

安装LightGBM依赖包

1

pip install lightgbm

LightGBM分类和回归

LightGBM有两大类接口：LightGBM原生接口 和 scikit-learn接口 ，并且LightGBM能够实现分类和回归两种任务。

基于LightGBM原生接口的分类

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score, accuracy_score
import lightgbm as lgb

# 加载数据
iris = datasets.load_iris()

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3)

# 转换为Dataset数据格式
train_data = lgb.Dataset(X_train, label=y_train)
validation_data = lgb.Dataset(X_test, label=y_test)

# 参数
params = {
    'learning_rate': 0.1,
    'lambda_l1': 0.1,
    'lambda_l2': 0.2,
    'max_depth': 4,
    'objective': 'multiclass',  # 目标函数
    'num_class': 3,
}

# 模型训练
gbm = lgb.train(params, train_data, valid_sets=[validation_data])

# 模型预测
y_pred = gbm.predict(X_test)
y_pred = [list(x).index(max(x)) for x in y_pred]
print(y_pred)

# 模型评估
print(accuracy_score(y_test, y_pred))

基于Scikit-learn接口的分类

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

from lightgbm import LGBMClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.externals import joblib

# 加载数据
iris = load_iris()
data = iris.data
target = iris.target

# 划分训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.2)

# 模型训练
gbm = LGBMClassifier(num_leaves=31, learning_rate=0.05, n_estimators=20)
gbm.fit(X_train, y_train, eval_set=[(X_test, y_test)], early_stopping_rounds=5)

# 模型存储
joblib.dump(gbm, 'loan_model.pkl')
# 模型加载
gbm = joblib.load('loan_model.pkl')

# 模型预测
y_pred = gbm.predict(X_test, num_iteration=gbm.best_iteration_)

# 模型评估
print('The accuracy of prediction is:', accuracy_score(y_test, y_pred))

# 特征重要度
print('Feature importances:', list(gbm.feature_importances_))
# Feature importances: [28, 6, 97, 61]

# 网格搜索，参数优化
estimator = LGBMClassifier(num_leaves=31)
param_grid = {
    'learning_rate': [0.01, 0.1, 1],
    'n_estimators': [20, 40]
}
gbm = GridSearchCV(estimator, param_grid)
gbm.fit(X_train, y_train)
print('Best parameters found by grid search are:', gbm.best_params_)
# Best parameters found by grid search are: {'learning_rate': 0.1, 'n_estimators': 20}

基于LightGBM原生接口的回归

对于LightGBM解决回归问题，我们用Kaggle比赛中回归问题：House Prices: Advanced Regression Techniques，地址：https://www.kaggle.com/c/house-prices-advanced-regression-techniques 来进行实例讲解。

该房价预测的训练数据集中一共有列，第一列是Id，最后一列是label，中间列是特征。这列特征中，有列是分类型变量，列是整数变量，列是浮点型变量。训练数据集中存在缺失值。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

import pandas as pd
from sklearn.model_selection import train_test_split
import lightgbm as lgb
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import Imputer

# 1.读文件
data = pd.read_csv('./dataset/train.csv')

# 2.切分数据输入：特征 输出：预测目标变量
y = data.SalePrice
X = data.drop(['SalePrice'], axis=1).select_dtypes(exclude=['object'])

# 3.切分训练集、测试集,切分比例7.5 : 2.5
train_X, test_X, train_y, test_y = train_test_split(X.values, y.values, test_size=0.25)

# 4.空值处理，默认方法：使用特征列的平均值进行填充
my_imputer = Imputer()
train_X = my_imputer.fit_transform(train_X)
test_X = my_imputer.transform(test_X)

# 5.转换为Dataset数据格式
lgb_train = lgb.Dataset(train_X, train_y)
lgb_eval = lgb.Dataset(test_X, test_y, reference=lgb_train)

# 6.参数
params = {
    'task': 'train',
    'boosting_type': 'gbdt',  # 设置提升类型
    'objective': 'regression',  # 目标函数
    'metric': {'l2', 'auc'},  # 评估函数
    'num_leaves': 31,  # 叶子节点数
    'learning_rate': 0.05,  # 学习速率
    'feature_fraction': 0.9,  # 建树的特征选择比例
    'bagging_fraction': 0.8,  # 建树的样本采样比例
    'bagging_freq': 5,  # k 意味着每 k 次迭代执行bagging
    'verbose': 1  # <0 显示致命的, =0 显示错误 (警告), >0 显示信息
}

# 7.调用LightGBM模型，使用训练集数据进行训练（拟合）
# Add verbosity=2 to print messages while running boosting
my_model = lgb.train(params, lgb_train, num_boost_round=20, valid_sets=lgb_eval, early_stopping_rounds=5)

# 8.使用模型对测试集数据进行预测
predictions = my_model.predict(test_X, num_iteration=my_model.best_iteration)

# 9.对模型的预测结果进行评判（平均绝对误差）
print("Mean Absolute Error : " + str(mean_absolute_error(predictions, test_y)))
# Mean Absolute Error : 55355.984107934746

基于Scikit-learn接口的回归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import pandas as pd
from sklearn.model_selection import train_test_split
import lightgbm as lgb
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import Imputer

# 1.读文件
data = pd.read_csv('./dataset/train.csv')

# 2.切分数据输入：特征 输出：预测目标变量
y = data.SalePrice
X = data.drop(['SalePrice'], axis=1).select_dtypes(exclude=['object'])

# 3.切分训练集、测试集,切分比例7.5 : 2.5
train_X, test_X, train_y, test_y = train_test_split(X.values, y.values, test_size=0.25)

# 4.空值处理，默认方法：使用特征列的平均值进行填充
my_imputer = Imputer()
train_X = my_imputer.fit_transform(train_X)
test_X = my_imputer.transform(test_X)

# 5.调用LightGBM模型，使用训练集数据进行训练（拟合）
# Add verbosity=2 to print messages while running boosting
my_model = lgb.LGBMRegressor(objective='regression', num_leaves=31, learning_rate=0.05, n_estimators=20,
                             verbosity=2)
my_model.fit(train_X, train_y, verbose=False)

# 6.使用模型对测试集数据进行预测
predictions = my_model.predict(test_X)

# 7.对模型的预测结果进行评判（平均绝对误差）
print("Mean Absolute Error : " + str(mean_absolute_error(predictions, test_y)))
# Mean Absolute Error : 29071.590700672827

LightGBM调参

控制参数

核心参数

IO参数

调参

下表对应了 Faster Speed ，better accuracy ，over-fitting 三种目的时，可以调的参数：

CatBoost

简介

CatBoost是俄罗斯的搜索巨头 Yandex 在2017年开源的机器学习库，也是Boosting族算法的一种，同前面介绍过的XGBoost和LightGBM类似，依然是在GBDT算法框架下的一种改进实现，是一种基于对称决策树（oblivious trees）算法的参数少、支持类别型变量和高准确性的GBDT框架，主要说解决的痛点是高效合理地处理类别型特征，这个从它的名字就可以看得出来，CatBoost是由catgorical和boost组成，另外是处理梯度偏差（Gradient bias）以及预测偏移（Prediction shift）问题，提高算法的准确性和泛化能力。

与XGBoost、LightGBM相比，CatBoost的创新点有：

• 嵌入了自动将类别型特征处理为数值型特征的创新算法。首先对categorical features做一些统计，计算某个类别特征（category）出现的频率，之后加上超参数，生成新的数值型特征（numerical features）。
• Catboost还使用了组合类别特征，可以利用到特征之间的联系，这极大的丰富了特征维度。
• 采用排序提升的方法对抗训练集中的噪声点，从而避免梯度估计的偏差，进而解决预测偏移的问题。
• 采用了完全对称树作为基模型。

类别型特征

类别型特征的相关工作

所谓类别型特征，即这类特征不是数值型特征，而是离散的集合，比如省份名（山东、山西、河北等），城市名（北京、上海、深圳等），学历（本科、硕士、博士等）。在梯度提升算法中，最常用的是将这些类别型特征转为数值型来处理，一般类别型特征会转化为一个或多个数值型特征。

如果某个类别型特征基数比较低（low-cardinality features），即该特征的所有值去重后构成的集合元素个数比较少，一般利用One-hot编码方法将特征转为数值型。One-hot编码可以在数据预处理时完成，也可以在模型训练的时候完成，从训练时间的角度，后一种方法的实现更为高效，CatBoost对于基数较低的类别型特征也是采用后一种实现。

显然，在高基数类别型特征（high cardinality features） 当中，比如 user ID，这种编码方式会产生大量新的特征，造成维度灾难。一种折中的办法是可以将类别分组成有限个的群体再进行One-hot编码。一种常被使用的方法是根据目标变量统计（Target Statistics，以下简称TS）进行分组，目标变量统计用于估算每个类别的目标变量期望值。甚至有人直接用TS作为一个新的数值型变量来代替原来的类别型变量。重要的是，可以通过对TS数值型特征的阈值设置，基于对数损失、基尼系数或者均方差，得到一个对于训练集而言将类别一分为二的所有可能划分当中最优的那个。在LightGBM当中，类别型特征用每一步梯度提升时的梯度统计（Gradient Statistics，以下简称GS）来表示。虽然为建树提供了重要的信息，但是这种方法有以下两个缺点：

• 增加计算时间，因为需要对每一个类别型特征，在迭代的每一步，都需要对GS进行计算；
• 增加存储需求，对于一个类别型变量，需要存储每一次分离每个节点的类别；

为了克服这些缺点，LightGBM以损失部分信息为代价将所有的长尾类别归为一类，作者声称这样处理高基数类别型特征时比One-hot编码还是好不少。不过如果采用TS特征，那么对于每个类别只需要计算和存储一个数字。

因此，采用TS作为一个新的数值型特征是最有效、信息损失最小的处理类别型特征的方法。TS也被广泛应用在点击预测任务当中，这个场景当中的类别型特征有用户、地区、广告、广告发布者等。接下来着重讨论TS，暂时将One-hot编码和GS放一边。

目标变量统计（Target Statistics）

CatBoost算法的设计初衷是为了更好的处理GBDT特征中的categorical features。在处理 GBDT特征中的categorical features的时候，最简单的方法是用 categorical feature 对应的标签的平均值来替换。

在决策树中，标签平均值将作为节点分裂的标准。这种方法被称为 Greedy Target-based Statistics , 简称 Greedy TS，用公式来表达就是： $$ \hat x_k^{i} = \frac {\sum_{j=1}^n[x_{j,k} = x_{i,k}] * Y_i}{\sum_{j=1}^n[x_{j,k} = x_{i,k}]} $$

这种方法有一个显而易见的缺陷，就是通常特征比标签包含更多的信息，如果强行用标签的平均值来表示特征的话，当训练数据集和测试数据集数据结构和分布不一样的时候会出条件偏移问题。

一个标准的改进 Greedy TS的方式是添加先验分布项，这样可以减少噪声和低频率类别型数据对于数据分布的影响： $$ \hat x_k^i = \frac {\sum_{j=1}^{p-1}[x_{\sigma_{j,k}} = x_{\sigma_{p,k}}]Y_{\sigma_j} + a * p}{\sum_{j=1}^{p-1}[x_{\sigma_{j,k}} = x_{\sigma_{p,k}}] + a} $$

其中 p 是添加的先验项， a 通常是大于 0 的权重系数。添加先验项是一个普遍做法，针对类别数较少的特征，它可以减少噪声数据。对于回归问题，一般情况下，先验项可取数据集label的均值。对于二分类，先验项是正例的先验概率。利用多个数据集排列也是有效的，但是，如果直接计算可能导致过拟合。CatBoost利用了一个比较新颖的计算叶子节点值的方法，这种方式（oblivious trees，对称树）可以避免多个数据集排列中直接计算会出现过拟合的问题。

当然，在论文《CatBoost: unbiased boosting with categorical features》中，还提到了其它几种改进Greedy TS的方法，分别有：Holdout TS、Leave-one-out TS、Ordered TS。

特征组合

值得注意的是几个类别型特征的任意组合都可视为新的特征。例如，在音乐推荐应用中，我们有两个类别型特征：用户ID和音乐流派。如果有些用户更喜欢摇滚乐，将用户ID和音乐流派转换为数字特征时，根据上述这些信息就会丢失。结合这两个特征就可以解决这个问题，并且可以得到一个新的强大的特征。然而，组合的数量会随着数据集中类别型特征的数量成指数增长，因此不可能在算法中考虑所有组合。为当前树构造新的分割点时，CatBoost会采用贪婪的策略考虑组合。对于树的第一次分割，不考虑任何组合。对于下一个分割，CatBoost将当前树的所有组合、类别型特征与数据集中的所有类别型特征相结合，并将新的组合类别型特征动态地转换为数值型特征。CatBoost还通过以下方式生成数值型特征和类别型特征的组合：树中选定的所有分割点都被视为具有两个值的类别型特征，并像类别型特征一样被进行组合考虑。

CatBoost处理Categorical features总结

• 首先会计算一些数据的statistics。计算某个category出现的频率，加上超参数，生成新的numerical features。这一策略要求同一标签数据不能排列在一起（即先全是0之后全是1这种方式），训练之前需要打乱数据集。
• 第二，使用数据的不同排列（实际上是4个）。在每一轮建立树之前，先扔一轮骰子，决定使用哪个排列来生成树。
• 第三，考虑使用categorical features的不同组合。例如颜色和种类组合起来，可以构成类似于blue dog这样的特征。当需要组合的categorical features变多时，CatBoost只考虑一部分combinations。在选择第一个节点时，只考虑选择一个特征，例如A。在生成第二个节点时，考虑A和任意一个categorical feature的组合，选择其中最好的。就这样使用贪心算法生成combinations。
• 第四，除非向gender这种维数很小的情况，不建议自己生成One-hot编码向量，最好交给算法来处理。

克服梯度偏差

对于学习CatBoost克服梯度偏差的内容，提出了三个问题：

• 为什么会有梯度偏差？
• 梯度偏差造成了什么问题？
• 如何解决梯度偏差？

CatBoost和所有标准梯度提升算法一样，都是通过构建新树来拟合当前模型的梯度。然而，所有经典的提升算法都存在由有偏的点态梯度估计引起的过拟合问题。在每个步骤中使用的梯度都使用当前模型中的相同的数据点来估计，这导致估计梯度在特征空间的任何域中的分布与该域中梯度的真实分布相比发生了偏移，从而导致过拟合。为了解决这个问题，CatBoost对经典的梯度提升算法进行了一些改进，简要介绍如下。

许多利用GBDT技术的算法（例如，XGBoost、LightGBM），构建下一棵树分为两个阶段：选择树结构和在树结构固定后计算叶子节点的值。为了选择最佳的树结构，算法通过枚举不同的分割，用这些分割构建树，对得到的叶子节点计算值，然后对得到的树计算评分，最后选择最佳的分割。两个阶段叶子节点的值都是被当做梯度或牛顿步长的近似值来计算。在CatBoost中，第一阶段采用梯度步长的无偏估计，第二阶段使用传统的GBDT方案执行。既然原来的梯度估计是有偏的，那么怎么能改成无偏估计呢？

设 $F_i$ 为构建i 棵树后的模型，$g^i(X_k,Y_k)$ 为构建 i棵树后第k 个训练样本上面的梯度值。为了使得$g^i(X_k,Y_k)$ 无偏于模型 $F_i$ ，我们需要在没有$X_k$ 参与的情况下对模型 进行训练。由于我们需要对所有训练样本计算无偏的梯度估计，乍看起来对于$F_i$ 的训练不能使用任何样本，貌似无法实现的样子。我们运用下面这个技巧来处理这个问题：对于每一个样本 $X_k$，我们训练一个单独的模型 $M_k$，且该模型从不使用基于该样本的梯度估计进行更新。我们使用$M_k$ 来估计 $X_k$ 上的梯度，并使用这个估计对结果树进行评分。用伪码描述如下，其中 $Loss(y_i, a)$ 是需要优化的损失函数， y 是标签值， a 是公式计算值。

预测偏移和排序提升

预测偏移

对于学习预测偏移的内容，提出了两个问题：

• 什么是预测偏移？
• 用什么办法解决预测偏移问题？

预测偏移（Prediction shift）是由梯度偏差造成的。在GDBT的每一步迭代中, 损失函数使用相同的数据集求得当前模型的梯度, 然后训练得到基学习器, 但这会导致梯度估计偏差, 进而导致模型产生过拟合的问题。CatBoost通过采用排序提升 （Ordered boosting） 的方式替换传统算法中梯度估计方法，进而减轻梯度估计的偏差，提高模型的泛化能力。下面我们对预测偏移进行详细的描述和分析。

首先来看下GBDT的整体迭代过程：

GBDT算法是通过一组分类器的串行迭代，最终得到一个强学习器，以此来进行更高精度的分类。它使用了前向分布算法，弱学习器使用分类回归树（CART）。

假设前一轮迭代得到的强学习器是 $F^{t-1}(x)$ , 损失函数是$L(y, F^{t-1}(x))$ ，则本轮迭代的目的是找到一个CART回归树模型的弱学习器 $h^t$，让本轮的损失函数最小。下面的式子表示的是本轮迭代的目标函数 $h^t$ 。 $$ h^t = \arg \min_{h\in H}EL((y,F^{t-1}(x) + h(x))) $$ GBDT使用损失函数的负梯度来拟合每一轮的损失的近似值，下面式子中$g^t(x,y)$ 表示的是上述梯度。 $$ g^t(x,y) = \frac {\partial L(y,s)}{\partial s}|_{s=F^{t-1}(x)} $$ 通常用下式近似拟合$h^t$. $$ h^t = \arg \min_{h\in H}E(-g^t(x,y) - h(x))^2 $$ 最终得到本轮的强学习器，如式（4）所示： $$ F^t(x) = F^{t-1}(x) + h^t $$ **在这个过程当中，偏移是这样发生的：**

根据 D\${X_k}$ 进行随机计算的条件分布$g^t(X_k, y_k)|X_k$ 与测试集的分布$g^t(X,y)|X$ 发生偏移，这样由公式（3）定义的基学习器 与公式（1）定义的产生偏差，最后影响模型 $F^t$ 的泛化能力。

排序提升

为了克服预测偏移问题，CatBoost提出了一种新的叫做Ordered boosting的算法。

由上图的Ordered boosting算法可知，为了得到无偏梯度估计, CatBoost对每一个样本 都会训练一个单独的模型 ，模型 由使用不包含样本的训练集训练得到。我们使用 来得到关于样本的梯度估计，并使用该梯度来训练基学习器并得到最终的模型。

Ordered boosting算法好是好，但是在大部分的实际任务当中都不具备使用价值，因为需要训练 个不同的模型，大大增加的内存消耗和时间复杂度。在CatBoost当中，我们以决策树为基学习器的梯度提升算法的基础上，对该算法进行了改进。

前面提到过，在传统的GBDT框架当中，构建下一棵树分为两个阶段：选择树结构和在树结构固定后计算叶子节点的值。CatBoost主要在第一阶段进行优化。在建树的阶段，CatBoost有两种提升模式，Ordered和Plain。Plain模式是采用内建的ordered TS对类别型特征进行转化后的标准GBDT算法。Ordered则是对Ordered boosting算法的优化。两种提升模式的具体介绍可以翻看论文《CatBoost: unbiased boosting with categorical features》。

快速评分

CatBoost使用对称树（oblivious trees）作为基预测器。在这类树中，相同的分割准则在树的整个一层上使用。这种树是平衡的，不太容易过拟合。梯度提升对称树被成功地用于各种学习任务中。在对称树中，每个叶子节点的索引可以被编码为长度等于树深度的二进制向量。这在CatBoost模型评估器中得到了广泛的应用：我们首先将所有浮点特征、统计信息和独热编码特征进行二值化，然后使用二进制特征来计算模型预测值。

基于GPU实现快速训练

• 密集的数值特征。 对于任何GBDT算法而言，最大的难点之一就是搜索最佳分割。尤其是对于密集的数值特征数据集来说，该步骤是建立决策树时的主要计算负担。CatBoost使用oblivious 决策树作为基模型，并将特征离散化到固定数量的箱子中以减少内存使用。就GPU内存使用而言，CatBoost至少与LightGBM一样有效。主要改进之处就是利用了一种不依赖于原子操作的直方图计算方法。
• 类别型特征。 CatBoost实现了多种处理类别型特征的方法，并使用完美哈希来存储类别型特征的值，以减少内存使用。由于GPU内存的限制，在CPU RAM中存储按位压缩的完美哈希，以及要求的数据流、重叠计算和内存等操作。通过哈希来分组观察。在每个组中，我们需要计算一些统计量的前缀和。该统计量的计算使用分段扫描GPU图元实现。
• 多GPU支持。 CatBoost中的GPU实现可支持多个GPU。分布式树学习可以通过数据或特征进行并行化。CatBoost采用多个学习数据集排列的计算方案，在训练期间计算类别型特征的统计数据。

CatBoost的优缺点

优点

• 性能卓越： 在性能方面可以匹敌任何先进的机器学习算法；
• 鲁棒性/强健性： 它减少了对很多超参数调优的需求，并降低了过度拟合的机会，这也使得模型变得更加具有通用性；
• 易于使用： 提供与scikit集成的Python接口，以及R和命令行界面；
• 实用： 可以处理类别型、数值型特征；
• 可扩展： 支持自定义损失函数；

缺点

• 对于类别型特征的处理需要大量的内存和时间；
• 不同随机数的设定对于模型预测结果有一定的影响；

实例

数据集

这里我使用了 2015 年航班延误的 Kaggle 数据集，其中同时包含类别型变量和数值变量。这个数据集中一共有约 500 万条记录，我使用了 1% 的数据：5 万行记录。数据集官方地址：https://www.kaggle.com/usdot/flight-delays#flights.csv 。以下是建模使用的特征：

• 月、日、星期： 整型数据
• 航线或航班号： 整型数据
• 出发、到达机场： 数值数据
• 出发时间： 浮点数据
• 距离和飞行时间： 浮点数据
• 到达延误情况： 这个特征作为预测目标，并转为二值变量：航班是否延误超过 10 分钟

实验说明： 在对 CatBoost 调参时，很难对类别型特征赋予指标。因此，同时给出了不传递类别型特征时的调参结果，并评估了两个模型：一个包含类别型特征，另一个不包含。如果未在cat_features参数中传递任何内容，CatBoost会将所有列视为数值变量。注意，如果某一列数据中包含字符串值，CatBoost 算法就会抛出错误。另外，带有默认值的 int 型变量也会默认被当成数值数据处理。在 CatBoost 中，必须对变量进行声明，才可以让算法将其作为类别型变量处理。

不加Categorical features选项的代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

import pandas as pd, numpy as np
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn import metrics
import catboost as cb

# 一共有约 500 万条记录，我使用了 1% 的数据：5 万行记录
# data = pd.read_csv("flight-delays/flights.csv")
# data = data.sample(frac=0.1, random_state=10)  # 500->50
# data = data.sample(frac=0.1, random_state=10)  # 50->5
# data.to_csv("flight-delays/min_flights.csv")

# 读取 5 万行记录
data = pd.read_csv("flight-delays/min_flights.csv")
print(data.shape)  # (58191, 31)

data = data[["MONTH", "DAY", "DAY_OF_WEEK", "AIRLINE", "FLIGHT_NUMBER", "DESTINATION_AIRPORT",
             "ORIGIN_AIRPORT", "AIR_TIME", "DEPARTURE_TIME", "DISTANCE", "ARRIVAL_DELAY"]]
data.dropna(inplace=True)

data["ARRIVAL_DELAY"] = (data["ARRIVAL_DELAY"] > 10) * 1

cols = ["AIRLINE", "FLIGHT_NUMBER", "DESTINATION_AIRPORT", "ORIGIN_AIRPORT"]
for item in cols:
    data[item] = data[item].astype("category").cat.codes + 1

train, test, y_train, y_test = train_test_split(data.drop(["ARRIVAL_DELAY"], axis=1), data["ARRIVAL_DELAY"],
                                                random_state=10, test_size=0.25)

cat_features_index = [0, 1, 2, 3, 4, 5, 6]


def auc(m, train, test):
    return (metrics.roc_auc_score(y_train, m.predict_proba(train)[:, 1]),
            metrics.roc_auc_score(y_test, m.predict_proba(test)[:, 1]))


# 调参，用网格搜索调出最优参数
params = {'depth': [4, 7, 10],
          'learning_rate': [0.03, 0.1, 0.15],
          'l2_leaf_reg': [1, 4, 9],
          'iterations': [300, 500]}
cb = cb.CatBoostClassifier()
cb_model = GridSearchCV(cb, params, scoring="roc_auc", cv=3)
cb_model.fit(train, y_train)
# 查看最佳分数
print(cb_model.best_score_)  # 0.7088001891107445
# 查看最佳参数
print(cb_model.best_params_)  # {'depth': 4, 'iterations': 500, 'l2_leaf_reg': 9, 'learning_rate': 0.15}

# With Categorical features，用最优参数拟合数据
clf = cb.CatBoostClassifier(eval_metric="AUC", depth=4, iterations=500, l2_leaf_reg=9,
                            learning_rate=0.15)

clf.fit(train, y_train)

print(auc(clf, train, test))  # (0.7809684655761157, 0.7104617034553192)

有Categorical features选项的代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

import pandas as pd, numpy as np
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn import metrics
import catboost as cb

# 读取 5 万行记录
data = pd.read_csv("flight-delays/min_flights.csv")
print(data.shape)  # (58191, 31)

data = data[["MONTH", "DAY", "DAY_OF_WEEK", "AIRLINE", "FLIGHT_NUMBER", "DESTINATION_AIRPORT",
             "ORIGIN_AIRPORT", "AIR_TIME", "DEPARTURE_TIME", "DISTANCE", "ARRIVAL_DELAY"]]
data.dropna(inplace=True)

data["ARRIVAL_DELAY"] = (data["ARRIVAL_DELAY"] > 10) * 1

cols = ["AIRLINE", "FLIGHT_NUMBER", "DESTINATION_AIRPORT", "ORIGIN_AIRPORT"]
for item in cols:
    data[item] = data[item].astype("category").cat.codes + 1

train, test, y_train, y_test = train_test_split(data.drop(["ARRIVAL_DELAY"], axis=1), data["ARRIVAL_DELAY"],
                                                random_state=10, test_size=0.25)

cat_features_index = [0, 1, 2, 3, 4, 5, 6]


def auc(m, train, test):
    return (metrics.roc_auc_score(y_train, m.predict_proba(train)[:, 1]),
            metrics.roc_auc_score(y_test, m.predict_proba(test)[:, 1]))


# With Categorical features
clf = cb.CatBoostClassifier(eval_metric="AUC", one_hot_max_size=31, depth=4, iterations=500, l2_leaf_reg=9,
                            learning_rate=0.15)
clf.fit(train, y_train, cat_features=cat_features_index)

print(auc(clf, train, test))  # (0.7817912095285117, 0.7152541135019913)

CatBoost与XGBoost、LightGBM的联系与区别

（1）2014年3月XGBoost算法首次被陈天奇提出，但是直到2016年才逐渐著名。2017年1月微软发布LightGBM第一个稳定版本。2017年4月Yandex开源CatBoost。自从XGBoost被提出之后，很多文章都在对其进行各种改进，CatBoost和LightGBM就是其中的两种。

（2）CatBoost处理类别型特征十分灵活，可直接传入类别型特征的列标识，模型会自动将其使用One-hot编码，还可通过设置 one_hot_max_size参数来限制One-hot特征向量的长度。如果不传入类别型特征的列标识，那么CatBoost会把所有列视为数值特征。对于One-hot编码超过设定的one_hot_max_size值的特征来说，CatBoost将会使用一种高效的encoding方法，与mean encoding类似，但是会降低过拟合。处理过程如下：

• 将输入样本集随机排序，并生成多组随机排列的情况；
• 将浮点型或属性值标记转化为整数；
• 将所有的类别型特征值结果都根据以下公式，转化为数值结果；

$$ avg_target = \frac {countInClass + prior}{totalCount + 1} $$

其中 countInClass 表示在当前类别型特征值中有多少样本的标记值是；prior 是分子的初始值，根据初始参数确定。totalCount 是在所有样本中（包含当前样本）和当前样本具有相同的类别型特征值的样本数量。

LighGBM 和 CatBoost 类似，也可以通过使用特征名称的输入来处理类别型特征数据，它没有对数据进行独热编码，因此速度比独热编码快得多。LighGBM 使用了一个特殊的算法来确定属性特征的分割值。

1

train_data = lgb.Dataset(data, label=label, feature_name=['c1', 'c2', 'c3'], categorical_feature=['c3'])

注意，在建立适用于 LighGBM 的数据集之前，需要将类别型特征变量转化为整型变量，此算法不允许将字符串数据传给类别型变量参数。

XGBoost 和 CatBoost、 LighGBM 算法不同，XGBoost 本身无法处理类别型特征，而是像随机森林一样，只接受数值数据。因此在将类别型特征数据传入 XGBoost 之前，必须通过各种编码方式：例如，序号编码、独热编码和二进制编码等对数据进行处理。

集成学习